Punch line: the risk of insolvency has the potential to significantly disrupt projected cash-flow streams and going-concern value and, commensurately, the modeling and valuation of risky ventures.
Investing in risky projects where projected cash-flows and going-concern value are subject to significant uncertainty involves modeling and pricing for the inherent risk of bankruptcy. The following stylized illustration provides a rudimentary simulation-based valuation framework where insolvency risk has the potential to significantly disrupt the “base-case” projected cash-flow stream.
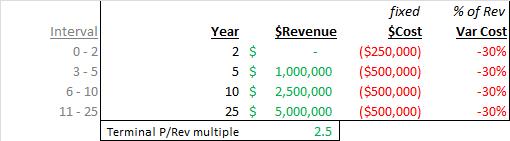
To set the stage, assume the following “base-case” 4-phase revenue-cost curve; 3 transition states (year 0-2, 3-5 and 6-10) and a final steady state to maturity (year 11-25); additionally, a terminal value multiple to reflect cash-flow to “perpetuity.” Costs are split into fixed costs (lease, rent, equipment, fees, permits, insurance etc.) and variable costs (100% – gross margin %). These assumptions are reflected in the table below:
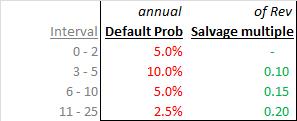
Next, in order to introduce the potential for bankruptcy to disrupt projected operations, consider the following “hump-backed” default-probability curve along with salvage-value/recovery multiples. These are reflected in the table below:
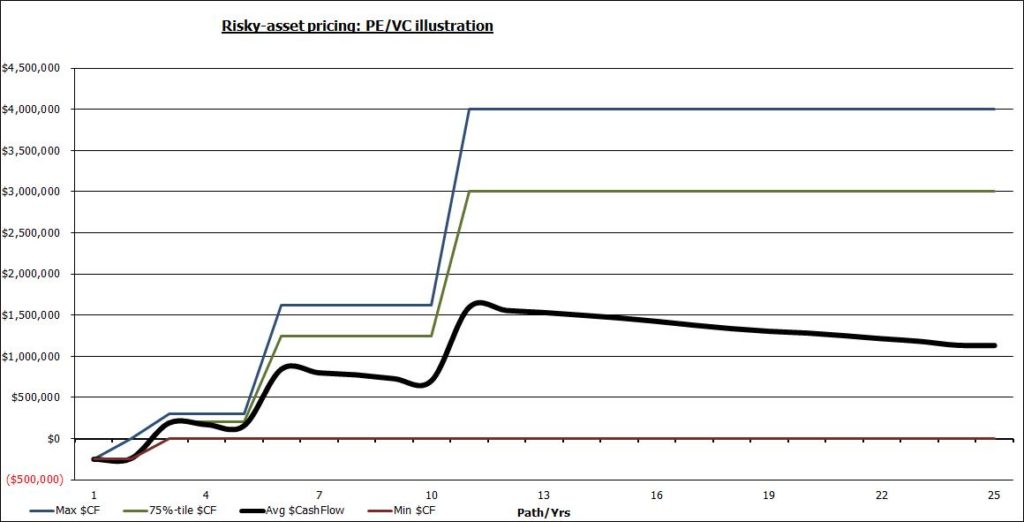
Next, in order to reflect the cash-flow impact of potential insolvency, populate a 1000×25 matrix (1000 paths of 25 annums each) with random draws from a standardized normal distribution and use that to trigger bankruptcy, or not, per the specifications above and accordingly simulate annual cash-flows along each path, accounting for the path dependency of prior outcomes. (For e.g. if a random draw of -2.1 occurs in year 13 then, since it’s worse than the z-value threshold level associated with the 2.5% default-probability assumption, the firm goes belly-up voiding future cash-flows (save salvage-value). These cash-flow dynamics are illustrated in the chart below (bold black line is the expected-value path):
Next, assuming a healthy discount rate** (UST 10y + incremental risk premium/OAS; 8% all-in this illustration), compute the present value of the cash-flows along each path. This is reflected in the frequency chart below with the long-left tail highlighting the cash-flow impact from bankruptcy:
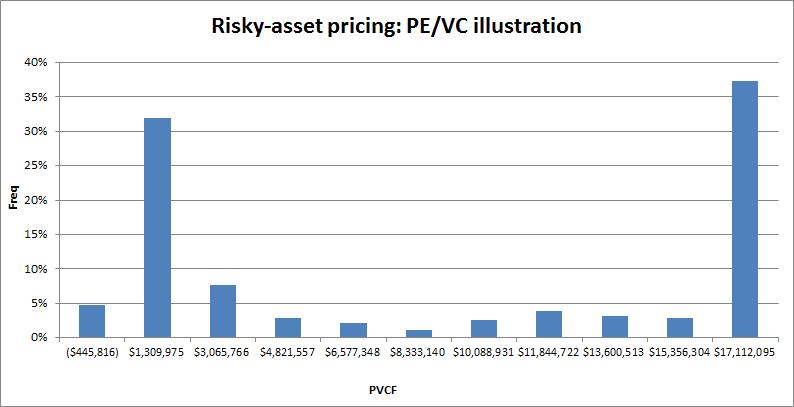
Aggregating, the average of the present value of the path cash-flow streams represents the potential valuation of this risky investment in a simulation-based risky world. Additionally, to illustrate the potential for sampling error, we can also compute the 95% confidence range around the expected valuation (95% of the time the true expected value, population mean, lies between a 2-sigma range).
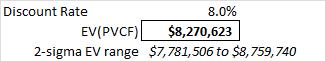
Using this simulation-based valuation along with the standard no-default, base-case cash-flow stream yields conventional IRR:

Finally, in the spirit of sensitivity analysis, the following table represents the NPV sensitivity to multiples of the base-line default-probability curve:

In summation, the above analysis provides a rudimentary framework for risk-return decision-making under uncertainty and underscores the importance of probabilistic valuation given the potential for insolvency to introduce significant dispersion in projected cash-flow streams and going-concern value; potentially serving as an additional pricing tool in the stable of valuation metrics.
** discount rate: theoretically, default-adjusted cash-flows should be discounted at the term risk-free rate (similar to option pricing) as they’ve been defanged of risk. However, additional risks (illiquidity, constrained demand, exit hurdle etc.) warrant an incremental risk premium/OAS (option-adjusted spread) to compensate for the enhanced set of risks embraced.
Note: calculations Risk Advisors
Proprietary and confidential to Risk Advisors
